Le mot d’André Knops, chercheur au CNRS et concepteur du module 1 :

« Il existe chez l’être humain, dès l’enfance, une capacité à percevoir et à traiter les quantités de manière approximative. Avec l’âge, cette perception se fait de plus en plus précise. La compréhension des procédures symboliques, telles que l’addition ou la soustraction, et la compréhension du nombre sont fondées sur cette capacité innée de perception et de traitement des quantités. À partir de ce constat, il s’agit dans un premier temps d’affiner la perception des quantités et donc le "sens du nombre", par exemple en faisant comparer des quantités non symboliques, représentées sous forme de nuages de points. Ensuite, il est nécessaire de renforcer le lien entre symboles et quantités : pour cela, on demandera d’associer une représentation non symbolique d’une quantité (un nuage de points) à une expression symbolique (un chiffre). Enfin, le concept de ligne numérique lie sens du nombre et de l’espace en amenant l’élève à se représenter spatialement une quantité. Pour travailler cette spatialisation des quantités, on peut par exemple demander à l’élève de placer une quantité ou un nombre sur une ligne numérique. Ces trois piliers qui forment notre approche cognitive requièrent une dernière capacité qui n’est pas spécifique au domaine des mathématiques, mais transversale : la capacité à se contrôler pour inhiber une tendance à répondre. Lorsqu’on compare deux nombres, 92 et 59, les unités donnent une information incompatible (2 < 9) avec le résultat de la comparaison (92 > 59). Lorsque deux informations sont incompatibles comme ici, l’élève doit se concentrer sur la dimension à comparer (celle des dizaines dans cet exemple), et laisser de côté les unités. Un tel exercice entraine la capacité de l’élève à laisser de côté les informations non pertinentes pour la réponse. »

Comment sont organisés les objectifs dans le module 1 ?

En s’appuyant sur les capacités innées des enfants et sur les apports de l’approche cognitive décrits ci-dessus, le Module 1 vise à faire acquérir des savoirs fondamentaux aux élèves : le principe de cardinalité, le principe de décomposition, l’ordinalité, et la relation entre quantité et symbole. Le contenu proposé dans chaque objectif du Module 1 correspond aux attendus et aux repères annuels pour chaque niveau du cycle 2 : CP, CE1 et CE2.

Quelques exemples illustrés 

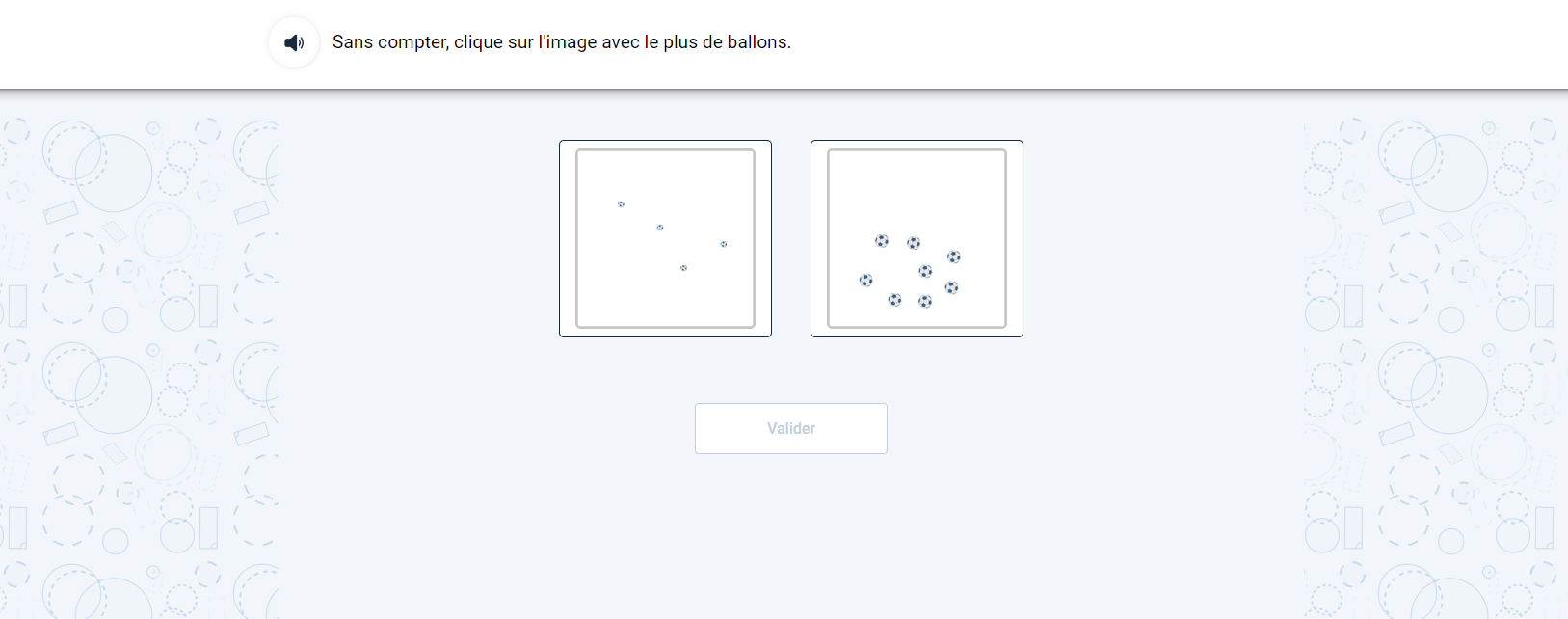
Objectif 1 : Comparer des collections comprenant 1 à 20 objets. 

Démarche du chercheur : Estimer et comparer intuitivement et globalement des quantités non symboliques dans des collections comprenant de 1 à 20 objets.

Difficultés visées : Dissocier impression de quantité (volontairement induite par des incongruences : taille des objets, densité du nuage, etc.) et numérosité des objets. 

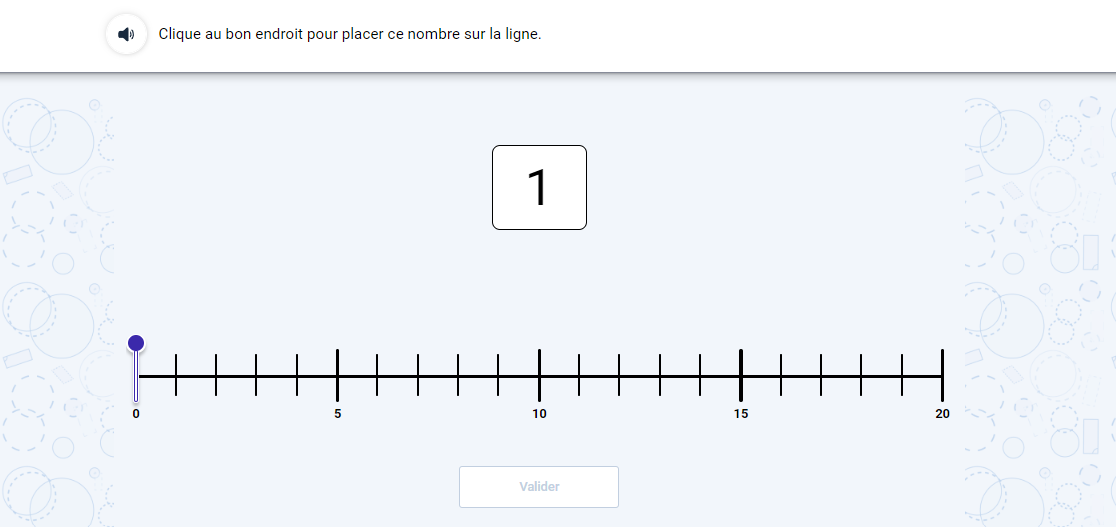
Objectif 4 : Positionner des nombres entiers entre 0 et 20 sur une demi-droite graduée

Démarche du chercheur : (se) représenter de manière symbolique un nombre compris entre 0 et 20, en lui associant une position spatiale sur une ligne numérique. 

Difficultés visées : Faire le lien entre sens du nombre et sens de l'espace sur une droite graduée de 5 en 5, puis sur une droite non graduée.